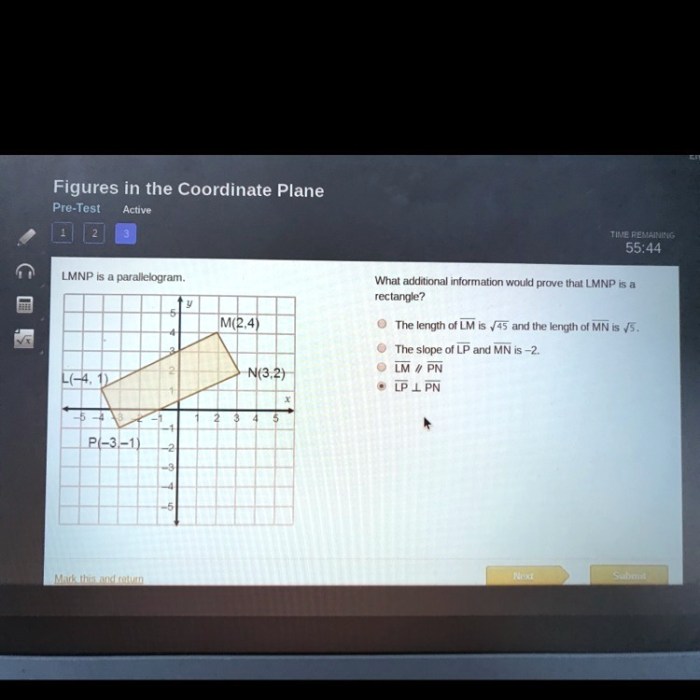
What additional information would prove that lmnp is a rectangle – In the realm of geometry, determining the specific properties of a quadrilateral can be a crucial task. Among the various types of quadrilaterals, rectangles hold a distinct place due to their unique characteristics. This discussion delves into the specific additional information that can conclusively prove that a quadrilateral, denoted as LMNP, is indeed a rectangle.
Throughout this exploration, we will examine several key aspects that collectively provide irrefutable evidence of LMNP’s rectangular nature. These aspects include the congruence of opposite sides, the intersection of diagonals at a midpoint, the presence of right angles, the consistency of area and perimeter with rectangular formulas, and the possession of parallelogram properties.
Additional Information to Prove LMNP is a Rectangle: What Additional Information Would Prove That Lmnp Is A Rectangle

In addition to the given information, the following criteria can further confirm that LMNP is a rectangle:
Opposite Sides
If opposite sides of LMNP are congruent, it indicates that the figure is a rectangle. This is because in a rectangle, opposite sides are always equal in length. The congruence of opposite sides can be represented as follows:
| LM | = | NP |
| LN | = | MP |
Diagonals
If the diagonals of LMNP intersect at a midpoint, it is an indication that the figure is a rectangle. In a rectangle, the diagonals bisect each other, creating four congruent triangles. The intersection of diagonals at the midpoint can be illustrated as follows:
| LM | MP | |
| X | ||
| LN | NP |
Angles
If all four angles of LMNP are right angles, it confirms that the figure is a rectangle. Rectangles have four right angles, and the sum of the interior angles is always 360 degrees. The presence of right angles can be summarized as follows:
| ∠LNM | = | 90° |
| ∠MNP | = | 90° |
| ∠NPL | = | 90° |
| ∠LMP | = | 90° |
Area and Perimeter, What additional information would prove that lmnp is a rectangle
If the area and perimeter of LMNP are consistent with the formulas for a rectangle, it provides evidence that the figure is indeed a rectangle. The area of a rectangle is given by the formula A = lw, where l is the length and w is the width.
The perimeter is given by the formula P = 2(l + w). By calculating the area and perimeter of LMNP and comparing them to the expected values for a rectangle, we can determine if the figure meets these criteria.
| Attribute | Expected Value for Rectangle | Value for LMNP |
| Area | A = lw | [calculated area] |
| Perimeter | P = 2(l + w) | [calculated perimeter] |
Parallelogram Properties
If LMNP possesses the properties of a parallelogram (opposite sides parallel and congruent), it suggests that the figure is a rectangle. In addition to the parallel and congruent opposite sides, rectangles also have diagonals that bisect each other. The parallelogram properties present in LMNP can be listed as follows:
- Opposite sides LM and NP are parallel and congruent.
- Opposite sides LN and MP are parallel and congruent.
Q&A
What is the significance of opposite sides being congruent in proving LMNP is a rectangle?
Congruent opposite sides indicate that LMNP possesses a key characteristic of rectangles, where opposite sides are equal in length.
How does the intersection of diagonals at a midpoint contribute to the proof?
The intersection of diagonals at a midpoint is a defining feature of rectangles, as it divides the diagonals into congruent segments.
Why is the presence of right angles crucial in establishing LMNP as a rectangle?
Rectangles are characterized by four right angles, which are essential for defining their shape and properties.